GYROSCOPES ET GYROMÈTRES

GYROSCOPES ET GYROMÈTRES

En 1852, Léon Foucault inventa un appareillage mécanique susceptible de mettre en évidence certains effets de la rotation de la Terre, et qu’il baptisa pour cette raison gyroscope . L’élément principal en était le rotor, corps solide de révolution tournant à grande vitesse autour de son axe, ce dernier conservant une certaine liberté cinématique, fonction de l’expérience à réaliser.

À l’heure actuelle, on appelle gyroscope tout appareil comprenant un rotor (ou toupie) tournant à grande vitesse autour de son axe , ce dernier possédant, suivant les cas, un ou deux degrés de liberté par rapport au boîtier de l’appareil. Dans les gyroscopes libres (ou 2 axes), peut se déplacer, par rapport au boîtier, dans un angle solide entourant un axe Z lié au boîtier, appelé axe de zéro; dans certains cas, cet angle solide couvre tout l’espace, par exemple dans le gyroscope à toupie sphérique portée par champ électrique. Dans les gyroscopes 1 axe, est astreint à balayer un plan fixe lié au boîtier.

À la fin du XIX^e siècle, Henry Bessemer (1875) puis Ernst Otto Schlick tentaient de lutter contre le roulis des navires en utilisant des gyroscopes de grandes dimensions; ces essais aboutirent au stabilisateur Sperry (1923), qui fut installé avec succès sur un paquebot de 41 000 tonnes. Lourds et encombrants, ces systèmes seront abandonnés au profit de pilotes automatiques , dans lesquels le rôle du gyroscope est limité à la détection du mouvement angulaire du véhicule, la stabilisation étant obtenue par des nageoires asservies. Cependant, à l’heure actuelle, l’effet stabilisateur des gyroscopes est exploité dans des dispositifs mettant en jeu de faibles inerties (plates-formes stabilisées, satellites artificiels, etc.).

Au début du XX^e siècle, certains industriels (Hermann Anschütz, Elmer Ambrose Sperry) appliquèrent les propriétés des gyroscopes à la recherche du nord géographique à bord des navires. Ainsi apparurent les compas gyroscopiques (ou gyrocompas), dont le fonctionnement s’est progressivement amélioré, pour aboutir aux appareillages actuels; leur précision est de l’ordre de quelques dixièmes de degré.

Par ailleurs, les progrès de l’aviation ont rapidement montré la nécessité de repères angulaires capables d’un fonctionnement autonome. Les gyroscopes furent à nouveau mis à contribution; il en est résulté l’apparition d’appareils simples et ingénieux: le directionnel et l’horizon artificiel, qui sont encore largement utilisés. Cependant, à bord des avions importants, tels le Concorde, le Boeing 747, l’Airbus A 340, de nombreux avions de combat, les lanceurs spatiaux, les accélérations et les vitesses atteintes perturbent leur fonctionnement; il y a lieu, dans ce cas, pour obtenir une référence angulaire correcte, d’installer une centrale de navigation inertielle à plate-forme gyrostabilisée ou à composants liés (ce dernier dispositif est qualifié de strapdown ; cf. systèmes de NAVIGATION, fig. 6).

Enfin, certains laboratoires ont étudié divers dispositifs de mesure des rotations absolues ne présentant qu’une analogie assez lointaine avec les gyroscopes classiques. Ce sont les gyroscopes à vibrations , dans lesquels le mouvement de rotation de la toupie est remplacé par le mouvement de va-et-vient d’éléments mécaniques; les gyroscopes nucléaires , dans lesquels le spin du noyau atomique est utilisé comme référence spatiale; les gyromètres optiques , exploitant les propriétés de la lumière cohérente, qui ont seuls abouti à des réalisations pratiques.

Le phénomène gyroscopique

Considérons une toupie t (synonyme de rotor) portée par un anneau A (fig. 1 et 2). Le comportement et les réactions de cette toupie lorsqu’elle est en rotation rapide autour de son axe peuvent être assez facilement compris en admettant les approximations suivantes ^{[cf. CINÉMATIQUE]}:

– son moment cinétique で est parallèle à , en raison de la grande vitesse de rotation de t autour de (plusieurs centaines de tours par seconde dans les appareils gyroscopiques modernes);

– le module de で est constant, car le couple résultant appliqué de A sur t admet une composante nulle suivant ; cette particularité est due à l’absence de frottement dans la liaison (At), ou encore à la compensation d’un couple de frottement par un moteur (électrique, pneumatique, etc.).

Il en résulte que で peut être considéré comme un vecteur lié à et à A. Dans ces conditions, l’application du théorème du moment cinétique à la toupie conduit à ぢ^a = (d で)/(dt ) (C ^a est le couple appliqué à t; (d で)/(dt ) est la vitesse absolue de で), soit:

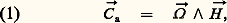où , dérive (ou précession) de t sous l’action de ぢ^a, est la rotation instantanée de A (ou de ).

En outre, d’après le principe de l’action et de la réaction, nous avons:

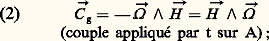ぢ^g est le couple gyroscopique induit par .

Les relations 1 et 2 décrivent des phénomènes pouvant paraître quelque peu déconcertants. En effet, considérons l’action d’un couple ぢ^a appliqué successivement à une toupie initialement immobile et à une toupie en rotation rapide autour de son axe . Dans le premier cas, la réaction de la toupie semble naturelle: elle se met à tourner autour d’un axe parallèle à ぢ^a; et un mouvement uniformément accéléré correspond à un couple ぢ^a constant. Dans le second cas, au contraire, on constate une précession autour d’un axe perpendiculaire à ぢ^a et à (et non plus parallèle à ぢ^a); de plus, cette précession se fait à vitesse constante lorsque ぢ^a admet un module constant et une direction perpendiculaire à (fig. 3).

En pratique, on cherche à donner à H une valeur aussi grande que possible, compte tenu de limitations en masse, en dimensions et en vitesse angulaire par rapport à . Il en résulte d’une part une faible vitesse de rotation de (de 10^-4 degré par heure à quelques degrés par heure) lorsqu’on prend soin de suspendre la toupie en minimisant le couple appliqué; cette propriété permet aux gyroscopes de jouer le rôle de repère angulaire . Il en résulte d’autre part la nécessité d’appliquer un couple ぢ^a important pour obtenir une précession notable de ; cette propriété permet aux gyroscopes de jouer un rôle stabilisateur .

Le phénomène gyroscopique est illustré par divers jouets: la toupie, le diabolo, le «gyroscope», le cerceau, etc. Par exemple, pour maintenir horizontal l’axe de rotation d’un diabolo sans limitation de durée, malgré les diverses perturbations, il faut lui appliquer un couple vertical , dans le sens convenable; dans le cas d’un utilisateur droitier, le moment cinétique obtenu est normalement dirigé vers l’arrière; si l’on constate une inclinaison de l’axe du diabolo vers l’avant, il faut donc, pour rétablir la situation, lui appliquer un couple vertical descendant: ce résultat peut être obtenu en reculant la baguette droite par rapport à la baguette gauche.

Gyroscopes libres

Le problème essentiel consiste à suspendre la toupie en minimisant l’incertitude Csur le couple qui lui est appliqué. L’ingéniosité des inventeurs et l’importance des recherches technologiques ont favorisé l’apparition de multiples réalisations parmi lesquelles on peut citer:

– la suspension par cardan , équipée de roulements à billes de haute précision; en laboratoire, la dérive de ce type d’appareils (sous l’action de C 轢) est de l’ordre de quelques degrés par heure; ce type de suspension est utilisé dans les directionnels (fig. 4) et les horizons gyroscopiques (fig. 5);

– la suspension par flottaison ; la poussée d’Archimède, agissant sur les anneaux de cardan et sur un carter étanche renfermant la toupie, soulage les paliers, qui peuvent alors être équipés d’ensembles pivot-rubis; les performances atteignent quelques centièmes de degré par heure;

– la suspension hydrodynamique ; la rotation de la toupie, agissant sur le gaz ambiant, provoque des surpressions équilibrant son poids; en fonctionnement, la toupie n’est soumise à aucune usure mécanique (performances de un à quelques centièmes de degré par heure);

– la suspension électrique ; la toupie, sphérique, est placée entre des électrodes, soumises à des potentiels électriques la maintenant en «lévitation» (performances meilleures que 10^-4 degré par heure);

– La suspension élastique (fig. 6); la toupie est reliée au boîtier par des éléments élastiques dont la raideur et l’inertie doivent vérifier une relation, dans laquelle entre la vitesse de rotation de la toupie; le respect de cette condition annule le couple transmis à la toupie; la précision est de un à quelques millièmes de degré par heure.

Tous ces appareils sont équipés de détecteurs d’écart, permettant de mesurer, à chaque instant, la position angulaire relative de l’axe de la toupie par rapport au boîtier. Ils comportent souvent, de plus, des «moteurs-couples», permettant d’appliquer à la toupie des couples connus, dans le but de compenser certains couples perturbateurs ou encore d’obtenir de la toupie une précession déterminée.

Gyroscopes «1 axe»

Les gyroscopes 1 axe (fig. 2) sont essentiellement constitués:

– d’une toupie t tournant autour d’un axe ; l’entraînement est en général effectué par un moteur électrique; l’ordre de grandeur du moment cinétique obtenu est de 10^-3 à 10^-1 kg.m²/s;

– d’un élément de cardan A (anneau ou carter) reliant au boîtier de l’appareil, par l’intermédiaire de l’axe de sortie S;

– d’un détecteur d’écart fournissant un signal électrique représentant la position angulaire ^g de A par rapport au boîtier;

– d’un moteur-couple permettant d’appliquer un couple 臨 ^g ひ à A en prenant appui sur le boîtier de l’appareil ( ひ est un vecteur unitaire porté par S).

De plus, ils comportent éventuellement:

– un liquide amortisseur dans lequel baigne un carter étanche contenant la toupie; il en résulte l’application à ce carter d’un couple «visqueux» 漣 f ^g ((d ^g)/(dt )) ひ, f ^g étant un coefficient constant; en outre, la flottaison ainsi obtenue permet de soulager la liaison boîtier-carter, qui peut alors être constituée par des ensembles pivot-rubis;

– un rappel élastique, dispositif mécanique ou électromécanique appliquant à A, en prenant appui sur le boîtier, un couple 漣 k ^{g g} ひ, k ^g étant un coefficient constant.

Les dimensions des gyroscopes 1 axe (quelques centimètres), leur masse (de 50 à 500 g), leur résistance mécanique (ils peuvent en général supporter des accélérations de 5 à 50 g ) autorisent leur utilisation à bord des véhicules les plus variés (avions, fusées, satellites, etc.).

L’application du théorème du moment cinétique à l’équipage mobile (A + t), avec projection sur ひ, conduit à la relation suivante, valable dans l’approximation des petits mouvements:

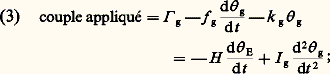(d ^E)/(dt ) est la composante de rotation instantanée du boîtier, autour de l’axe d’entrée E perpendiculaire à S et à ; I ^g est le moment d’inertie de l’équipage mobile, par rapport à S (de l’ordre de 10^-6 à 10^-4 kg.m²).

Cette relation permet d’étudier la réaction de ce type d’appareil à une petite rotation (d ^E)/(dt ) autour de E. Différents cas sont à envisager.

Si f ^g = 0, k ^g = 0, la relation (3) se réduit à:

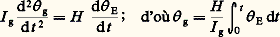[on a admis: ^g (0) = 0; ((d ^E)/(dt )) (0) = 0 et 臨 ^g = 0].

La lecture ^g est ici proportionnelle à 咽t 0 ^E dt ; l’appareil est appelé gyroscope intégrateur. La liaison (A-boîtier) peut être réalisée par roulements à billes ou par palier fluide.

Si f ^g 0, k ^g = 0, la relation (3) devient:

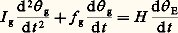(on admet 臨 ^g = 0), soit, en régime permanent:

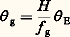[on admet ^g (0) = ^E (0) = 0].

La lecture ^g est ici proportionnelle à ^E; le coefficient constant H /f ^g est le gain statique, dont l’ordre de grandeur est de 1,5 à 6. Ce type d’appareil, appelé gyromètre intégrateur, est encore utilisé pour la stabilisation de plates-formes inertielles. Les performances sont de quelques millièmes à quelques dixièmes de degré par heure.

Si f ^g 0, k ^g 0, la relation (3) devient:

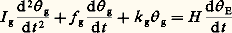(on admet que 臨 ^g est nul), soit, en régime permanent:

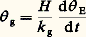[on admet ^g (0) = ^E (0) = 0].

La lecture ^g est ici proportionnelle à (d ^E)/(dt ). Les domaines de mesure de ces appareils, appelés gyromètres, sont très différents, suivant les cas; en effet, il y a lieu de distinguer entre les gyromètres de pilotage et les gyromètres de haute précision.

Les premiers, peu encombrants, relativement bon marché, dont le rappel élastique est souvent dû à un ressort, et dont l’étendue de mesure peut être de quelques degrés à quelques centaines de degrés par seconde, sont utilisés pour le pilotage automatique des avions, des fusées, des navires. Les seconds sont des appareils à équipage mobile porté par flottaison, dont le rappel est obtenu par un asservissement électromécanique. L’étendue de mesure de ces gyromètres peut varier, suivant les cas, de quelques degrés par heure à quelques degrés par seconde.

Gyrolasers et gyromètres à fibre optique

Les expériences de Georges Sagnac (1913) et d’Albert Abraham Michelson (1924) ont montré la possibilité d’effectuer des mesures de rotations absolues à partir d’expériences d’optique. La mise au point de cavités résonantes lasers, en circuit optique fermé, a permis, dans les années quatre-vingt, la réalisation de gyrolasers pouvant, dans une certaine mesure, concurrencer les gyromètres mécaniques.

La théorie de ces appareils, faisant intervenir la mécanique quantique et la relativité générale, est difficile (M. H. Soffel, 1989). Néanmoins, une première idée de leur principe de fonctionnement peut être obtenue par un raisonnement faisant appel à la cinématique classique.

Admettons (F. Aronowitz, 1971) qu’il soit licite de travailler sur un chemin optique circulaire de centre O (fig. 7 a). Lorsque le dispositif matérialisant ce chemin est immobile par rapport à l’espace absolu, nous sommes en présence d’ondes progressives, dans les sens horaire et anti-horaire, vérifiant une condition de la forme: périmètre 2 神 R = n (n est un nombre entier; est la longueur d’onde des signaux lumineux).

Quand ce dispositif est en rotation (par exemple anti-horaire, comme sur la figure 7 a), les chemins optiques horaire et anti-horaire se différencient; en effet, pour revenir à son point de départ (lié au bloc optique), le signal tournant dans le sens anti-horaire doit faire 1 tour + R 見 , alors que le signal tournant dans le sens horaire doit faire 1 tour 漣 R 見 .

Compte tenu des relations 見 = 諸 t et t = 2 神R /c (c est la vitesse de la lumière), les conditions de résonance deviennent: dans le sens anti-horaire, n ⁺ = 2 神R (1 + ((R 諸 )/c )); dans le sens horaire, n ^- = 2 神R (1 漣 ((R 諸 )/c )). Compte tenu des conditions 諸 t 廉 2 神 et f = c , il s’ensuit que les fréquences f des signaux anti-horaire et horaire ont une différence f telle que:

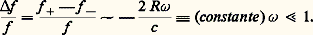Cette différence, proportionnelle à 諸 , peut être mesurée par méthode interférométrique, comme cela est indiqué schématiquement sur la figure 7 b. Les rayons arrivant en D, correspondant aux signaux anti-horaire et horaire, font un angle suffisamment petit (quelques minutes) afin que les franges obtenues soient assez larges (quelques millimètres), pour être détectées par un dispositif opto-électronique.

La rotation 諸 implique une cadence de défilement des franges, par rapport à D; il en résulte que chaque frange représente un quantum angulaire 嗀 bien défini, de l’ordre de quelques secondes d’angle dans le cas de chemins optiques de quelques dizaines de centimètres. Ces quanta représentent des microrotations absolues autour de l’axe d’entrée つ, perpendiculaire au plan du trajet optique et passant par O.

L’utilisation pratique de ces montages nécessite une activation mécanique consistant à faire osciller le bloc optique autour de つ, à une cadence de quelques centaines de hertz; cela a pour but d’éliminer le seuil important que présente naturellement l’appareil (J.-C. Radix, 1983).

Dans ces conditions, il est possible de réaliser des capteurs gyrométriques dont les performances sont caractérisées par une erreur de facteur d’échelle pouvant être inférieure à 10^-6, une dérive angulaire de l’ordre de quelques millièmes de degré par heure, pendant quelques heures, un domaine de mesure pouvant dépasser 360 degrés par seconde.

Ces caractéristiques ont notamment autorisé la réalisation de navigateurs inertiels (sans plate-forme stabilisée) destinés aux avions civils et militaires ainsi qu’à des lanceurs spatiaux comme Ariane IV et V.

Le principe des gyromètres à fibre optique consiste à effectuer une expérience d’interférométrie classique comparant les phases de deux signaux, initialement synchrones, et parcourant des trajets de types ABCA et ACBA (fig. 7 a). Soit t la durée nécessaire pour que la lumière fasse le tour du cercle (O, R ): t = 2 神R /c . La différence entre les chemins optiques horaire et anti-horaire est donc:

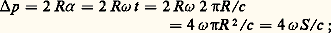S est l’aire limitée par les trajets optiques considérés. Examinons l’ordre de grandeur de S permettant de traduire une vitesse de rotation de 10 degrés par heure par un déphasage d’un quart de tour entre les deux signaux; nous devons avoir: p = /4 = c /4 f , d’où S = c p /4 諸 = c ²/16 諸 f . Avec = 0,6 猪m (rouge orangé), S = 22 500 mètres carrés! Cet ordre de grandeur donne une idée des installations très particulières que Michelson dut utiliser pour réaliser cette expérience et mettre en évidence, par ce procédé, l’influence de la rotation terrestre.

Par ailleurs, les besoins des systèmes de navigation concernent des appareils dont les dimensions sont au maximum de dix centimètres au cube et dont la sensibilité est meilleure que le degré par heure. Depuis 1976, de nombreuses études, effectuées par des universitaires et des industriels, ont permis de résoudre la difficulté signalée. Trois idées sont à la base de ce succès: l’utilisation de bobines de fibre optique (plusieurs milliers de tours), avec addition des efficacités dues à l’aire de chacune des spires (comme dans un solénoïde); la modulation des signaux optiques, de manière à linéariser la réponse du capteur au signal 諸 ; le fonctionnement du dispositif en appareil de zéro, en simulant l’application d’un signal très voisin de 漣 諸 .

Il en est résulté des montages dont un exemple est schématisé sur la figure 7 c. Le polariseur a pour but de diminuer le couplage indésirable entre les signaux horaire et anti-horaire. Le détecteur fournit des impulsions représentant chacune, comme dans le cas d’un gyrolaser, un quantum de rotation 嗀 de l’ordre de la seconde d’angle; la valeur de 嗀 peut être modifiée par voie électronique (il n’en est pas ainsi dans le cas du gyrolaser).

Les résultats obtenus par ce type d’appareil laissent espérer, pour un encombrement raisonnable, les performances suivantes: une dérive de quelques centièmes de degré par heure, une stabilité du facteur d’échelle de 5 . 10^-5, un domaine de mesure de 1 000 degrés par seconde. Il en résulte un nouveau type de capteur pouvant concurrencer le gyrolaser.

Encyclopédie Universelle. 2012.